Proc. IX Int. Conf. Electrical Bio-Impedance (Heidelberg), pp 532-535, 1995
RECONSTRUCTION OF ABSOLUTE CONDUCTIVITY DISTRIBUTION IN ELECTRICAL IMPEDANCE TOMOGRAPHY
A. V. Korjenevsky
Institute of Radioengineering and Electronics of Russian Academy of Sciences, Mokhovaya St., 11, Moscow, 103907, Russia
Fast algorithm of reconstruction of absolute conductivity distribution in a cross-section of human body by measurements of electrodes' potentials on the skin surface is described. The algorithm is based on the method of back projection along equipotential lines, but there is no need in a reference data set corresponding to the object of uniform conductivity.
Introduction
Electrical impedance tomograph (or applied potential tomograph - see (1)) shows promise but it does not become in a wide medical practice. It may be concerned with the fact that existing systems for electrical impedance imaging offer in vivo so-called dynamic image (visualization of the difference between two measurements). The medical professions prefer static or absolute images. In electrical impedance tomography, obtaining of such images is complicated as it is necessary to have reference set of data corresponding to the uniform conductivity object. So far as, in practice, electrodes of the tomograph are fixed directly on the patient's skin, it seems to be unlikely to obtain a reference set of measurements corresponding to body shape of a patient under each specific electrodes' distribution, neither by the use of a uniform-conductivity phantom of a required shape nor by numerical solution of straight problem with corresponding boundary conditions. The use of a container of cylindrical shape filled with conductive liquid, where patient is immersed, is also unsuitable and bringing to nought the advantages of the method: relative simplicity of medical examination and a minimum of patient's inconvenience. The multifrequency measurements and reconstruction method (2) while enables to visualize some static objects but it is really a differential method with respect to frequency (instead of time). The use of conventional and new methods of inverse problem solving (3) so far doesn't give satisfactory results at real conditions of absolute conductivity in vivo imaging. This paper describes fast algorithm for absolute conductivity reconstruction and results of its application.
Reconstruction algorithm
This algorithm is based on
the method of back projection between electric equipotential lines (1). Source
data are the potential differences between adjacent electrodes fixed on
patient's skin along a closed contour, while a pair of the electrodes being set
to current source. Let we have a reference data set which corresponds to a
preceding measurement (at a previous moment of time) - in the case of
differential tomography, or data set corresponding to measurements of uniform
object. Then the value of conductivity S (in conventional units) to be
assigned to a point of an image with polar coordinates r and 
under
reconstruction, can be calculated according to the formula (here we assume
cylindrical geometry of the object's boundary):
,
/1/
where i is number of pair of active electrodes (profile
number), W - weighting factor, 
- the result of
linear interpolation of the function:
,
of a discrete variable, 
and 
- measured
voltage at j-th pair of the electrodes
(j=2,.....,N-2, readings are taken from the active pair j=0
of a measurement) and reference voltage, respectively, argument x (0<x<N)
defines by the intersection of an electric field equipotential line passed
through the point 
with outside
boundary of an object, F(x)
and 
- the potential
distribution along the boundary and inside potential distribution for 0-th pair
of active electrodes for uniform conductivity object.
Then, we determine the
weighting factor W in /1/. Let we have a point-like (too small with
respect to the object to be tested) medium region having the conductivity other
than outside uniform medium. The region (we call it as sample object), while
current passes through the medium, is equivalent to an electric dipole which
momentum is proportional to its size, electric field strength, and conductivity
difference between the sample object and the medium. Such a dipole deforms a
potential distribution at the boundary. Specify W in such a way that,
the expression under the sum sign in /1/, would be independent from location of
the sample object if its conductivity remains unchanged. In the assumption of
point-like geometry of field source, we obtain by substitution of dipole field
intensity values instead of 
and 
:
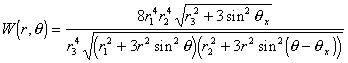
The coordinates system is chosen so that the boundary surface radius
equals to 1, active pair contacts' coordinates are:
, 
, receiving point (point of intersection of
equipotential line and object boundary): 
, 
; 
- distance from
active pair to 
point, 
- distance from
point to
receiving point, 
- distance from
active pair to receiving point. The normalization 
is used. The
weighting factor can be defined more exactly by taking into account a distance
between the electrodes (i.e. both the exciting and measuring dipoles are not a
point-like) thus enhancing the image reconstruction. There is no need to
calculate W during
reconstruction. The values to be found can be calculated separately and stored
in the form of table of size equal to the number of image elements. The
analogous table must contain values of x which determine the point on
boundary with the potential equal to one in a given point 
within the
object. When the object has non-cylindrical form, the inexact representation of
F(x)
and 
does not lead
to an essential worsening of an image.
The main problem under the
absolute image reconstruction is obtaining of reference data, corresponding to
the object with uniform conductivity and the same electrode positions. Our
approach is to approximate the measured data by more "smooth" curves
using modified least square method and a set of basal functions to obtain the
reference data set. The approximation should reproduce common features of the
original function but not the details which contain information about the
interior of an object investigated. It has been found that systematic errors
distort the measured values of potential differences. They are taking place,
mainly, due to spurious coupling in tomograph's integral multiplexers and input
circuits. In differential tomography these errors slightly affect on the
reconstruction, because the same error components are added both to reference
and main data and compensate each other. Nevertheless, during the absolute
conductivity reconstruction, artefacts appear due to the stray coupling thus
worsening image. To eliminate these effects, measured in a proper way stray
coupling signals should be included as part of basal functions used for
approximation. Clearly, the total number of basal functions can not be too
large because the approximation could not take into account superfluous
details. The best results are obtained when a combination of three functions is
used: 
- distribution
of voltage between adjacent electrodes along the border of a cylindrical object
of uniform conductivity while current source is hooked up to 0-th pair, 
and 
- the
tomograph's spurious signals for each active pair of electrodes i. The
potential distribution to be found is approximated by linear combination
,
where coefficients 
are determined
on weighing least-square criterion, i.e. by minimization of sum of squares of
discrepancies between approximating and approximated functions multiplied by properly
chosen weighting coefficients:
. /2/
The weighting coefficients 
make available
a proper dependence of approximation accuracy from approximating function
values. Selection
, /3/
ensures relative approximation error to be constant. The
reconstruction improves if we add 
as divisor
cofactor in /3/. The coefficients 
are obtained by
solving a system of linear algebraic equations taken from derivatives of /2/
equated to zero. The use of the reference data creation procedure described
above leads to an additional image filtration and improves resolution.
Results
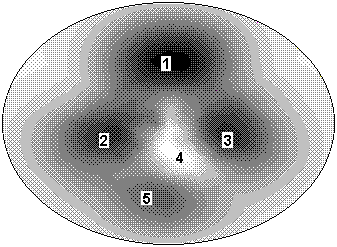
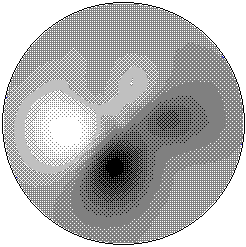
The method is used with 16 - electrodes electrical impedance tomograph. Measurements were accomplished with pulse current source. Input data set consists of 208 (13*16) measured values of voltage (reciprocity principle did not use, redundant data reduce errors). The tomograph design and running the measurements are described in (4). Image reconstruction was performed using polar grid with 16 radial and 32 angular node points. Redundant reconstructed points make possible averaging over neighbouring points that diminishes device errors. Reconstruction of a one image (without visualization) takes 0.04 sec using IBM-compatible PC with Intel 486 DX2-66 MHz processor. The device and algorithm were tested at in vitro application. Of course, the results of in vivo applications of absolute conductivity visualization are most interesting and we present it there. The measurements were made at different heights of human torso and on extremities. Fig. 1 shows the reconstructed conductivity distributions in volunteer's thorax cross-section and in the shank. The lighter areas in these images correspond to higher conductivity of tissues.
As we used the adaptive algorithm for reference data synthesis under image reconstruction, extraction of quantitative information from the reconstruction results at once proves to be impossible. Comparison of the different images concerning absolute conductivity is also difficult. For image normalization, we use known data on conductivity of such tissues as bone and blood (or muscle). Under the normalization, a point with minimum conductivity is defined in image, and bone conductivity (0.01 S/m) is assigned to it. Absolute conductivity value of 0.5 S/m is assigned to the point with maximum conductivity. All other values fall within this interval. After the calibration, the magnitude of lung tissue conductivity is in a good agreement with data of straight measurements (for example, given in (1)).
(a) (b)
Fig. 1. (a) Reconstructed conductivity distribution in a volunteer's thorax cross-section. Image was reconstructed under the assumption of cylindrical geometry of the object, then compressed in vertical direction for better subjective perception. Designated areas are identified as: 1 - spinal column, 2 - right lung, 3 - left lung, 4 - heart with its blood vessels, 5 - chest bone. (b) Reconstructed conductivity distribution in left shank cross-section. Dark areas correspond to big and small shinbones, light areas - blood vessels and muscles.
Conclusion
The algorithm of absolute conductivity reconstruction produces, with the help of the electrical impedance tomograph, both habitual for medical profession and rather informative absolute (or static) images. It shows a good outlook for practical use of electrical impedance tomography both in clinics and in medical researches. First results obtained under the reconstruction of absolute conductivity in vivo, are very promising.
References
1. Barber D C and Brown B H 1984 Applied Potential Tomography, J. Phys. E: Sci. Instrum. 17, pp 723-733
2. Griffits H and Ahmed A 1987 A dual-frequency applied potential tomography technique: computer simulations, Clin. Phys. Physiol. Meas. 8 Suppl. A, pp 103-108
3. Isaacson D, Cheney M and Newell J C 1992 Comments on reconstruction algorithms, Clin. Phys. Physiol. Meas. 13 Suppl. A, pp 83-89
4. Cherepenin V A, Korjenevsky A V, Kornienko V N, Kultiasov Y S and Kultiasov M Y 1995 The electrical impedance tomograph: new capabilities. This volume