IRE RAS. Laborartory of Electromagnetism & Antennas

Vesnik M.V.

Michael V. Vesnik, Dr. Sci. in Physics and Mathematics, Leading Researcher, vesnik@cplire.ru

Field of scientific interests: electromagnetic diffraction theory, heuristic solutions in diffraction theory, canonical problems in diffraction theory, electromagnetic waves propagation in complex media, reflector antennas.

Fields of research in the Laboratory of Electrodynamics	Main results of M. Vesnik
I. Electromagnetic waves propagation in complex media and structures
- electromagnetic scattering and diffraction	1. Jointly with P. Ya. Ufimtsev discovered a new asymptotic feature of corner waves scattered by polygonal plates [1, 2]. 2. Introduced a method of use 2-D solution in 3-D problems without integrations over elementary strips [3]. 3. Originated a new method in diffraction theory: a method of generalized eikonal (MGE) (¹) [4, 5]. With use of MGE obtained new solutions for electromagnetic diffraction on 2-D half plate [5] and truncated wedge [12]. Fundamentals of MGE are included into a book on heuristic methods in diffraction theory, materials of corresponding section of the book are prepared jointly with Yu. A. Kravtsov [6]. 4. Obtained heuristic (²) solution of canonical (³) problem of electromagnetic wave diffraction by plane angular sector [7]. 5. Developed a deterministic theory of wave propagation in urban media (⁴).
II. New types of transmission lines
- dielectric waveguides	6. Jointly with V. A. Kaloshin introduced an analytical solution for pattern calculation of a radiator representing an open end of a circular dielectric waveguide with metal screen (⁵) [8].
III. Antennas (50 МHz- 300 GHz)
- multibeam dual reflector antennas	7. Jointly with other colleagues from the laboratory took part in design of reflector antennas new types (⁶) [9, 10, 11].

Comments for footnotes

(¹). Method of generalized eikonal

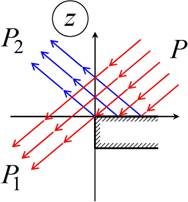
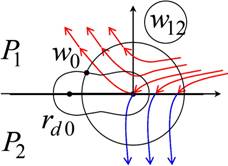
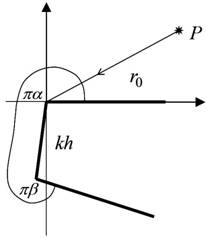
Consider an electromagnetic wave P propagating in 2-D unbounded space. Let us bring into this space a 2-D perfectly conducting half – infinite scatterer (Fig. 1). Consider conformal mapping kZ(w) of region w₁₂ (Fig. 2) upper half-plane onto region z that is the exterior of the scatterer (Fig. 1), k=2p/l is the wave number.

Fig. 1 Plane wave diffraction on a half-plane.

Fig. 2 Auxiliary region w₁₂.

Fig. 3 Cylindrical wave P diffraction on a half-plane.

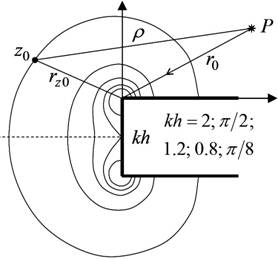
Fig. 4 Curves r_d₀ structure for different values of dimensional parameter kh. Exterior curves correspond to smaller kh values, inner curves correspond to larger kh values..

Integral representation of diffraction problem solution is constructed in domain of complex value ŵ representing an analytic continuation from the curves r_d₀ disposed in auxiliary region w₁₂. In so doing region w₁₂ transforms into region ŵ₁₂. On the curves r_d₀ (Fig. 2, 4) conformal transformation derivative module k|dZ(w)/dw| is a constant. In domain of complex value ŵ incident wave geometrical optics function P transforms into the function P^c.

Consider a closed contour encompassing “lighted” regions of the domain ŵ₁₂. Here “lighted” called regions of function P^c existence (in terms of geometrical optics) on the curve r_d₀. Let us call “shadowed” regions the regions of function P^c absence on the curve r_d₀. Then using Cauchy residue theorem in domain ŵ₁₂ one can construct an integral representation for the function P^c(ŵ) taken in observation point w₀ on the curve r_d₀:

, (1)

where K=1/0 if the point w₀ is inside/outside closed integration contour.

Let domain ŵ₁₂ contain areas where function P^c(ŵ) as wave number k decreases. These areas are referred to as convergence areas. Consider a region with two convergence areas s1 and s2. Denoting the sum of the integrals over s1 and s2 in (1) as v(w₀) and the integral over the remaining part of С as V(w₀), we obtain the expression:

. (2)

Integral representation (2) is rigorous and for the problem of edge diffraction is equivalent to known Sommerfeld’s integral representation. For the scatterers of more complicate shape integral representation (2) allows to obtain new solutions in diffraction theory [4, 5].

The method of generalized eikonal can be used both for rigorous solutions and for heuristic approaches.

(²). Heuristic approaches in diffraction theory

Mathematically rigorous diffraction theory analytical solutions can be obtained for a limited set of scatterers geometrical shapes allowing separation of variables.

In order to solve electrodynamics boundary value problems physics often use so called “heuristic” approaches. These solutions represent a set of analytical formulas and algorithms of their application. They are being used in a situation when rigorous analytical solution is absent and use of numerical solution is unreasonable due to, for instance, low operating speed or complicate interpretation of calculation results. Besides, numerical solution requires corresponding program packages and qualified programmers.

Without rigorous mathematical proof heuristic solutions are based on the understanding of diffraction phenomena physical nature and on general principles of electrodynamics such as field principle of locality, principle of complementarity, reciprocity principle. Sometimes heuristic solutions are based on physical intuition. For instance, in order to make solution satisfy periodicity conditions in two – sheet domain A. Sommerfeld intuitively introduced a multiplying factor function in the integrand of solution integral representation which was similar to expression (2) of this paper. Later correctness of this intuitive introduction had bee confirmed when the solution has been constructed in a different way, namely – with use of variables separation method.

As usual, heuristic solutions rigorous mathematical proof is absent. However, correctness of a heuristic solution is confirmed by comparison of numerical results, passage to the limit or by other means (for instance, by comparison with experimental results or by other reliable data). From the other side, comparison with known data itself allows to improve heuristic solution.

(³). Diffraction theory canonical problems

Canonical solutions (or model problems solutions) represent diffraction problems solutions for basic geometrical structures. Sometimes canonical solutions are also called “model” or “etalon” solutions. Solutions for basic geometrical structures are used in order to find heuristic solutions for objects of more complicate geometry.

Diffraction theory canonical problems solutions (half-plate [5] (Fig. 1, 3), cutted wedge (Fig. 5), plane angular sector [7] (Fig. 6)) can be obtained with use of heuristic approaches.

Fig. 5 Cutted wedge diffraction problem.

Fig. 6 Plane angular sector diffraction problem.

(⁴). Regular theory for electromagnetic wave propagation in urban media.

In contrast to stochastic theories for wave propagation in urban media new theory is regular. This theory takes into account diffraction and multiple reflection on such object of urban media as walls, windows, roofs, quoins, polyhedral angles generated by roofs and quoins. The approach combines elements of diffraction theory for wedges, model structures and rough surfaces, elements of wave propagation theory and elements of antenna theory.

The results of this theory can also be used for calculation of indoor wave propagation.

(⁵). Radiating element based on circular metal-dielectric waveguide.

Jointly with V.A. Kaloshin an analytical theory for a radiating element based on circular metal-dielectric waveguide is developed [8]. In order to find radiating pattern of this radiating element firstly waveguide modes are found by means of characteristic equation, secondly space integration of these modes is performed within physical optics approach. Comparison with experimental results has shown good agreement between the theory and experiment.

(⁶). New types of reflector antennas (*).

(*) Jointly with V. A. Kaloshin, A. S. Venetsky and E. V. Frolova.

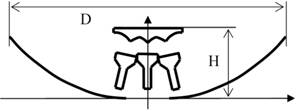
New types of dual reflector antennas were recently designed in Laboratory of electromagnetism. Dual reflector system “Toroidal” (Fig. 7) allows receiving signals from several TV satellites in wide angular domain (±20º) simultaneously and without turning antenna [9]. Compact multibeam reflector antenna [10] (Fig. 8) also allows receiving several satellite TV signals simultaneously and without antenna rotating. Compactness factor with a small value of H/D ratio (parameters H and D are shown on Fig. 8) makes it possible to create an antenna with design that allows using antenna indoor.

Fig. 7 Multibeam reflector antenna “Toroidal” with high aperture efficiency for each beam.

Fig. 8 Compact multibeam reflector antenna with less aperture efficiency than in antenna “Toroidal”, but with a better compactness factor H/D.

List of citations

[1]. M.V.Vesnik, P.Y.Ufimtsev, “An Asymptotic Feature of Corner Waves Scattered by Polygonal Plates”, Electromagnetics, Vol.12, NN 3-4, pp.265-272, Jul.-Dec. 1992

[2]. M.V. Vesnik "Elimination of Infinites in Diffraction Coefficients of Physical Optics Current's Components for a Shadow Contour of a Scatterer", Proceedings of the 1995 International Symposium on Electromagnetic Theory, pp. 407-409, St. Petersburg, Russia, May 23-26, 1995

[3] M.V. Vesnik “Use of Two-Dimensional Solutions in Three-Dimensional Problems”, Journal of Communications Technology and Electronics, 38(15), 1993, pp. 77-84.

[4]. M.V. Vesnik "Analytical solution for electromagnetic diffraction on 2-D perfectly conducting scatterers of arbitrary shape", IEEE Trans. Antennas Propagat., vol. 49, pp. 1638 - 1644, Dec. 2001

[5]. Vesnik M.V. «Use of the generalized eikonal in the analytic solution of the problem of electromagnetic-wave diffraction by a 2D perfectly conducting half-plate», Journal of Communications Technology and Electronics, 2008, Vol. 53, No. 2, pp. 131-142

[6]. M.Vesnik, Yu.A. Kravtsov, Section 5.1.7 Diffraction by Bodies with Wedges: Method of Generalised Eikonal (MGE) in the book: Yury A. Kravtsov, Ning Yan Zhu "Theory of Diffraction: Heuristic Approaches" Alpha Science International Ltd.Oxford, U.K., 2010

[7]. M.V. Vesnik «On a Possibility of Constructing a Refined Heuristic Solution for the Problem of Diffraction by a Plane Angular Sector», Journal of Communications Technology and Electronics, 2011, Vol. 56, No. 2, pp. 531-543

[8]. M.V. Vesnik, V.A. Kaloshin, «On the radiation from the open end of a circular metal-dielectric waveguide» (in Russian), Journal of Radio Electronics, 2001, No. 2 (electron journal) http://jre.cplire.ru/jre/feb01/4/text.html

[9]. V.A. Kaloshin, «Mirror antenna», Russian patent: RU 2173496 C1, publication date 10.09.2001, priority date 10.07.2000.

[10]. M.V. Vesnik, Jiho Ahn, E.V. Frolova, A.S. Venetskiy, «Compact Multibeam Mirror Antenna», Russian patent: RU 2380802 C1, publication date 27.01.2010, priority date 17.11.2008

[11] M. V. Vesnik, “On the Possibility of the Application of Axially Displaced Ellipse Antenna Elements for Construction of a Compact Multibeam Antenna System”, IEEE Antennas and Propagation Magazine, Vol. 53, No.2, April 2011, pp. 125-128

[12] M.V. Vesnik, «Analytical Solution for the 2D Diffraction of Electromagnetic Wave by a Truncated Wedge», Journal of Communications Technology and Electronics, 2012, Vol. 57, No. 10, pp. 1061–1072

- multibeam dual reflector antennas